Atomic and Nuclear Physics (Numerical Problems)
18.1. The half-life of is ![]() is 7.3 s. A sample of this nuclide of nitrogen is observed for 29.2 s. Calculate the fraction of the original radioactive isotope remaining after this time.
is 7.3 s. A sample of this nuclide of nitrogen is observed for 29.2 s. Calculate the fraction of the original radioactive isotope remaining after this time.
18.2. Cobalt-60 is a radioactive element with half-life of 5.25 years. What fraction of the original sample will be left after 26 years?
18.3. Carbon-14 has a half-life of 5730 years. How long will it take for the quantity of carbon-14 in a sample to drop to one-eighth of the initial quantity?
18.4. Technetium-99 m is a radioactive element and is used to diagnose brain, thyroid, liver and kidney diseases. This element has half-life of 6 hours. If there is 200 mg of this technetium present, how much will be left in 36 hours.
18.5. Half-life of a radioactive element is 10 minutes. If the initial count rate is 368 counts per minute, find the time for which count rates reaches 23 counts per minute.
| Count rate / minute | 400 | 200 | 100 | 50 | 25 |
| Time (in minutes) | 0 | 2 | 4 | 6 | 8 |
Plot a graph between the count rate and time in minutes. Measure the value for the half-life of the element from the graph.
18.7. A sample of certain radioactive element has a half-life of 1500 years. If it has an activity of 32000 counts per hour at the present time, then plot a graph of the activity of this sample over the period in which it will reduce to 1/16 of its present value.
18.8. Half-life of a radioactive element was found to be 4000 years. The count rates per minute for 8 successive hours were found to be 270, 280, 300, 310, 285, 290, 305, 312. What does the variation in count rates show? Plot a graph between the count rates and time in hours. Why the graph is a straight line rather than an exponential?
18.9. Ashes from a campfire deep in a cave show carbon-14 activity of only one-eighth the activity of fresh wood. How long ago was that campfire made?
18.1. The half-life of is ![]() is 7.3 seconds. A sample of this nuclide of nitrogen is observed for 29.2 s. Calculate the fraction of the original radioactive isotope remaining after this time.
is 7.3 seconds. A sample of this nuclide of nitrogen is observed for 29.2 s. Calculate the fraction of the original radioactive isotope remaining after this time.
Solution: Let half life of ![]() is T1/2 = 7.3 seconds
is T1/2 = 7.3 seconds
The original activity = A0
As after time T1/2 its activity will become A0/2
After 2 T1/2 = 2 x 7.3 = 14.6 seconds. The activity will become A0/4
After 3 T1/2 = 3 x 7.3 = 21.9 seconds. The activity will become A0/8
After 4 T1/2 = 4 x 7.3 = 28.2 seconds. The activity will become A0/16
Hence 1/16th of the original sample will be left.
18.2. Cobalt-60 is a radioactive element with half-life of 5.25 years. What fraction of the original sample will be left after 26 years?
Solution: Let half life of Cobalt -60 is T1/2 = 5.25 years
The original activity = A0
As after time T1/2 = 5.25 years. The activity will become A0/2
After time 2 T1/2 = 2 x 5.25 = 10.50 years. The activity will become A0/4
After time 3 T1/2 = 3 x 5.25 = 15.75 years. The activity will become A0/8
After time 4 T1/2 = 4 x 5.25 = 21.0 years. The activity will become A0/16
After time 5 T1/2 = 5 x 5.25 = 26.25 years. The activity will become A0/32
Hence after 26 years less than 1/32th of the original sample will be left.
18.3. Carbon-14 has a half-life of 5730 years. How long will it take for the quantity of carbon-14 in a sample to drop to one-eighth of the initial quantity?
Solution: Let half life of Cobalt -14 is T1/2 = 5730 years
As after time T1/2 = 5730 years. The activity will become A0/2
After time 2 T1/2 = 2 x 5730 = 11460 years. The activity will become A0/4
After time 3 T1/2 = 3 x 5730 = 17190 years. The activity will become A0/8
Hence 1/8th of the original sample will be left after the 1.72 x 104 years
18.4. Technetium-99 m is a radioactive element and is used to diagnose brain, thyroid, liver and kidney diseases. This element has half-life of 6 hours. If there is 200 mg of this technetium present, how much will be left in 36 hours.
Solution: Half life of Technetium = 6 hours
Mass (m0 =200 mg
How much left after time = 36 hours.
Mass of Technetium left after first half life T1/2 6 hours is 100 mg
Mass of Technetium left after 2nd half life 2 x T1/2 12 hours is 50 mg
Mass of Technetium left after 3rd half life 3 x T1/2 18 hours is 25 mg
Mass of Technetium left after 4th half life 4 x T1/2 24 hours is 12.5 mg
Mass of Technetium left after 5th half life 5 x T1/2 30 hours is 6.25 mg
Mass of Technetium left after 6th half life 6 x T1/2 36 hours is 3.12 mg
18.5. Half-life of a radioactive element is 10 minutes. If the initial count rate is 368 counts per minute, find the time for which count rates reaches 23 counts per minute.
Solution: Let half life of a radioactive element is T1/2 = 10mins
The original activity = A0 = 368 counts per minute.
As after first half time T1/2 = 10 mins
The activity will become A0/2 = 368/2 = 184 counts per minute
As after second half life time 2 x T1/2 = 2 x 10 = 20 mins
The activity will become A0/4 = 368/4 = 92 counts per minute
As after third half life time 3 x T1/2 = 3 x 10 = 30 mins
The activity will become A0/8 = 368/8 = 46 counts per minute
As after fourth half life time 4 x T1/2 = 4 x 10 = 40 mins
The activity will become A0/16 = 368/16 = 23 counts per minute
Hence after 40 minutes its count rate will be 23 counts per minute.
18.6. In an experiment to measure the half-life of a radioactive element, the following results were obtained:
| Count rate / minute | 400 | 200 | 100 | 50 | 25 |
| Time (in minutes) | 0 | 2 | 4 | 6 | 8 |
Plot a graph between the count rate and time in minutes. Measure the value for the half-life of the element from the graph.
Ans:
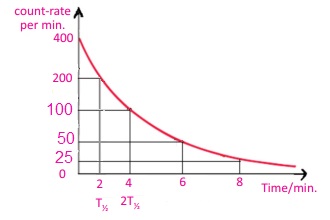
It half life T1/2 is 2 minutes
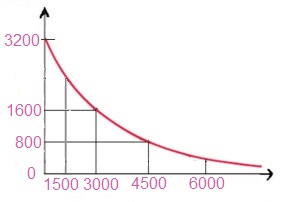
18.7. A sample of certain radioactive element has a half-life of 1500 years. If it has an activity of 32000 counts per hour at the present time, then plot a graph of the activity of this sample over the period in which it will reduce to 1/16 of its present value.
Solution: Given data:
Let half life of a radioactive element is T1/2 = 1500 years
The original activity = A0 = 3200 counts per minute.
First half life T1/2 = 1500 years, activity will be A0/2 = 3200/2 = 166 c/m
Second half life 2 x T1/2 = 2 x 1500 = 3000 years, activity will be A0/4 = 3200/4 = 800 c/m
Third half life 3 x T1/2 = 3 x 1500 = 4500 years, activity will be A0/8 = 3200/8 = 400 c/m
Fourth half life 4 x T1/2 = 4 x 1500 = 6000 years, activity will be A0/16 = 3200/16 = 200 c/m
| Count rate | 3200 | 1600 | 800 | 400 | 200 |
| Time (in years) | 0 | 1500 | 3000 | 4500 | 6000 |
18.8. Half-life of a radioactive element was found to be 4000 years. The count rates per minute for 8 successive hours were found to be 270, 280, 300, 310, 285, 290, 305, 312. What does the variation in count rates show? Plot a graph between the count rates and time in hours. Why the graph is a straight line rather than an exponential?
Ans: Variation in count rate shows the random nature of radioactive decay, graph is almost horizontal line rather than exponential curve which is due to long half-life as compared to period of 8 hours.
| Count rate | 270 | 280 | 300 | 310 | 285 | 290 | 305 | 315 |
| Time succ. 8 hours | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
18.9. Ashes from a campfire deep in a cave show carbon-14 activity of only one-eighth the activity of fresh wood. How long ago was that campfire made?
Solution: Given data:
We know half life of C-14 is T1/2 = 5730 years
Since the ratio has been reduced by 1/8 (one-eighth)
Therefore three half life have passed.
The age of the fossil is given by first half life T1/2 = 5730 years
Age of the fossil is given by after 2nd half life 2 x T1/2 = 2 x 5730 = 14160 years
Age of the fossil is given by after 3rd half life 3 x T1/2 = 3 x 5730 = 17190 years
<—————————–>