Unit 2 – Solving A Biological Problem (Exercise Questions)
Answer The Following Questions.
Q.1. Describe the steps involved in biological method taking malaria as an example.
Q.2. If a test show that some people have Plasmodium in their blood but they do not show any symptoms of malaria, what hypothesis would you formulate to answer this problems?
Q.3. How the principals of ratio and proportion are used in biological method.
Q.4. Justify mathematics as an integral part of the scientific process.
Short Questions-Text Exercise
Q.1. Differentiate between theory and law.
Q.2. Quantitative observation are better in biological method. How?
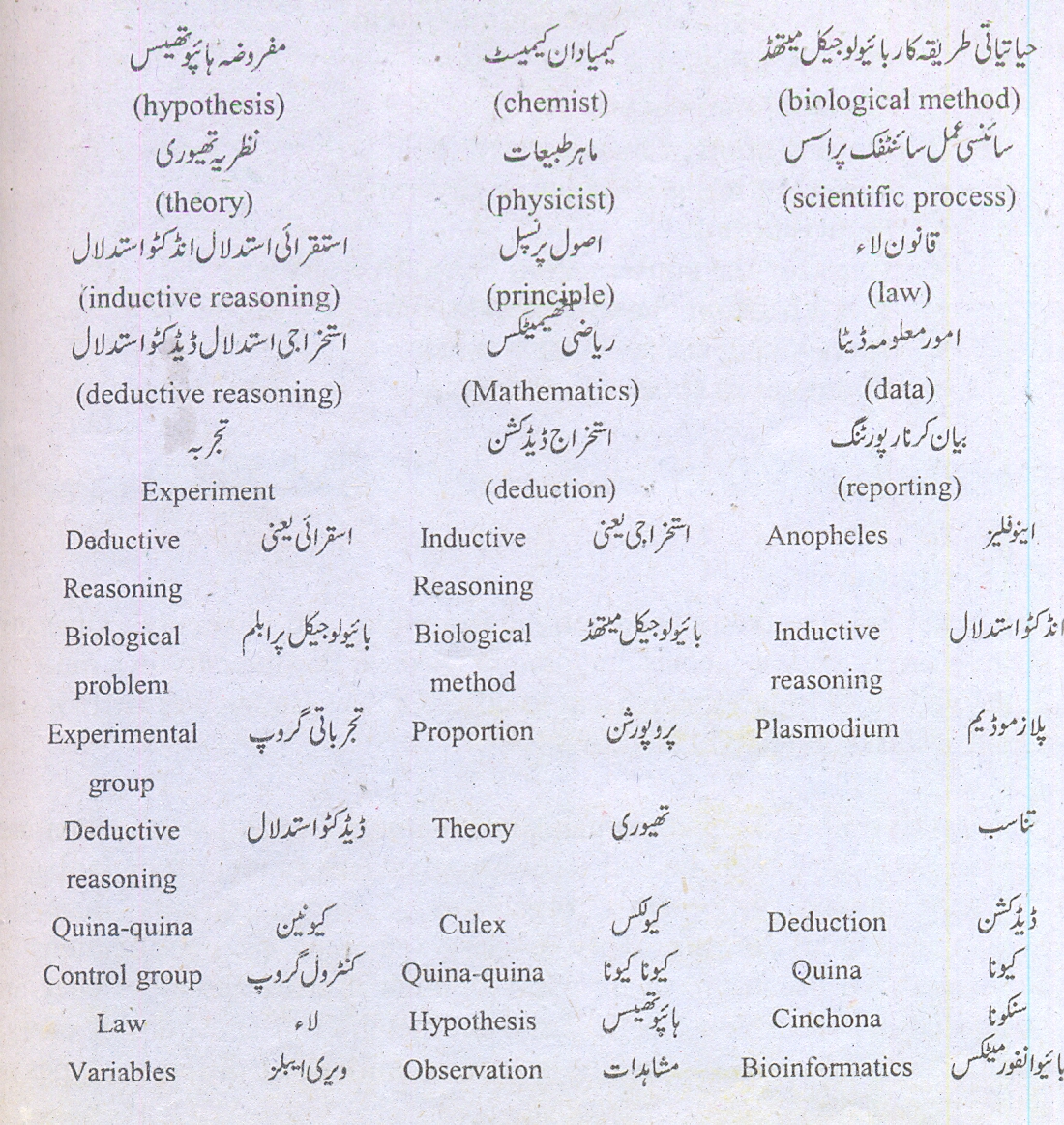
THE TERMS TO KNOW
Q.1. Describe the steps involved in biological method taking malaria as an example.
Answer:
Introduction:
Malaria has killed more people than any other disease. The account of malaria is an example of a biological problem and of how such problems are solved.
Malaria is a common disease in many countries including Pakistan.
Steps taken to solve this problem were as follows:
(i) Recognition of problem:
In ancient times (more than 2000 years ago), physicians were familiar with malaria. They described it as a disease of chills and fevers with recurring attacks
Observations about Malaria:
In the last part of 19th century many different causes of malaria were being suggested. By that time there were four major observations about malaria.
• Malaria and marshy areas have some relation.
• Quinine is an effective drug for treating malaria.
• Drinking water from marshes does not cause malaria.
• “Plasmodium’ is seen in the blood of malarial patients.
(iii) Hypothesis Formulation:
A scientist uses whatever information and observation he has and makes one or more hypotheses. The hypothesis made in this case was:
‘Plasmodium is the cause of malaria’.
(iv) Deductions:
A scientist does not know whether this hypothesis is true or not, but he accepts that it may be true and makes deductions. One of the deductions from the above hypothesis was:
If Plasmodium is the cause of malaria, then all persons ill with malaria should have Plasmodium in their blood’. Experimentation:
The next step was to test the deduction through experiments which were designed as follows:
Experimental Group:
Blood of 100 malarial patients was examined under microscope.
Control Group:
Blood of 100 healthy persons was examined under the microscope.
Results:
The experimental results showed that almost all malarial patients had Plasmodium in their blood while 7 out of 100 healthy persons also had Plasmodium in their blood. Plasmodium in the blood of healthy individuals was in its incubation period i.e. the period between the entry of parasite in the host and appearance of symptoms. The results were quite convincing and proved that the hypothesis, ‘Plasmodium is the cause of Malaria’ was true.
The next biological problem was to learn about How Plasmodium gets into the blood of a
man?’
(i) Observations
Biologists were having the following observations:
• Malaria is associated with marshes.
• Drinking water of marshes does not cause malaria.
From these observations, it can be concluded that Plasmodium was not in the marsh water. It must be carried by something that comes to marsh water.
Observations of A.F.A King:
(In 1883, a physician, A.F. A King, listed 20 observations: Some of his important observations were:
• People who slept outdoors were more likely to get malaria than those who slept indoors.
• People who slept under fine nets were less likely to get malaria than those who did not use such nets.
• Individuals who slept near a smoky fire usually did not get malaria.
(ii) Hypothesis
On the basis of his observations, King suggested a hypothesis:
‘Mosquitoes transmit Plasmodium and so are involved in the spread of malaria’.
(iii)Deductions
Following deductions were made considering the hypothesis as true.
(a) If mosquitoes are involved in the spread of malaria, then Plasmodium should be present in mosquitoes. ‘
(b) If mosquitoes are involved in the spread of malaria, then a mosquito can get Plasmodium by biting a malarial patient.’
(iv)Experiments of Ronald Ross
In order to test the above deductions, Ronald Ross, a British army physician working in India, in 1880’s, performed important experiments.
Experiment 1:
• He allowed a female Anopheles mosquito to bite a malarial patient.
• He killed the mosquito some days later.
• On examining the mosquito, Plasmodium was found multiplying in mosquito’s stomach.
Experiment 2:
The next logical experiment was to allow an infected mosquito (having Plasmodium) bite a healthy person. If the hypothesis was true, the healthy person would have got malaria. But scientists avoid using human beings for experiments when results can be so serious. Ross used sparrows and redesigned his experiments. He allowed a female Culex mosquito to bite the sparrows suffering from malaria.
• Some of the mosquitoes were killed and studied at various times.
• Ross found that Plasmodium multiplied in the wall of mosquito’s stomach and then moved into the mosquito’s salivary glands.
• He kept some of the mosquitoes alive and allowed them to bite healthy sparrows.
Results:
Ross found that saliva of the infected mosquitoes contained Plasmodia and these entered sparrow’s blood. When he examined the blood of these previously healthy sparrows, he found many Plasmodia in it.
Experimentation on Man:
In the end, the hypothesis was tested by direct experimentation on human beings. In 1898, Italian biologists took these steps for confirmation:
• They allowed an Anopheles mosquito to bite a malarial patient.
• The mosquito was kept for a few days
• Then it was allowed to bite a healthy man.
Results:
The person later became ill with malaria. In this way it was confirmed that mosquitoes transmit Plasmodium and spread Malaria.
Q.2. If a test show that some people have Plasmodium in their blood but they do not show any symptoms of malaria, what hypothesis would you formulate to answer this problems?
Answer:
Following hypothesis can be suggested to account for that many people and many birds with malarial parasite do not show the symptoms.
Hypothesis:
“Reproduction of malarial parasites in blood of cells result in the appearance of symptoms.” It means nmber of parasites was not sufficient to cause disease.
Q.3. How the principals of ratio and proportion are used in biological method.
Answer:
DATA ANALYSIS
Data analysis is necessary to prove or disprove a hypothesis by experimentation.
Statistical Methods:
Data analysis is done through application of statistical methods, i.e. ratio and proportion.
Ratio:
When a relation between two numbers e.g. “a’ and ‘b’ is expressed in terms of quotient (a/b) it is called the ratio of one number to the other.
Expression of a ratio:
A ratio is expressed by putting a division (:) or colon ( : ) mark between two numbers.
Example:
The ratio between 50 malarial patients and 150 normal patients is 1:3.
Proportion:
Proportion means to join two equal ratios by the sign of equality (=) Proportion may be expressed as a:b :: :d Example:
a:b = c:d is a proportion between the two ratios. This proportion may also be expressed as a:b :: c:d
Calculation of Fourth Value:
When three values in a proportion are known, the fourth one (X) can be calculated.
Example:
A biologist can calculate how many birds will get malaria when he allows infected mosquitoes to bite 100 healthy sparrows. In the previous experiment he noted that when he allowed mosquitoes to bite 20 sparrows, 14 out of them got malaria. Now he may apply the proportion rule:
1st Ratio: 14:20 (14 out of 20)
2nd Ratio: X: 100 (How many out of 100)
Proportion: 14:20 :: X: 100
X/100 = 14/20
X x 20 = 100 x 14
X= 100/20 x 14
X= 70
It means, 70 out of 100 sparrows would get malaria.
Importance of Statistics:
Statistics are thus a means of summarizing data through the calculation of a mean value. This step is very important as it transforms raw data into information, which can be used to summarize and report results.
Q.4. Justify mathematics as an integral part of the scientific process.
Answer:
Biological method involves the use of applied mathematics to solve biological
problems.
Mathematical Applications:
Major biological problems, in which knowledge of mathematics is used include:
• Gene finding
• Protein structure
• Protein-protein interactions
Bioinformatics:
Bioinformatics refers to the computational and statistical techniques for the analysis of biological data.
Short Questions-Text Exercise
Q.1. Differentiate between theory and law.
Answer:
Theory: The hypotheses that stand the test of time (often tested and never rejected), are called theories. A theory is supported by a great deal of evidence.
Law: If a theory survives such doubtful approach and continues to be supported by experimental evidence, it becomes a law or principal. A scientific law is a uniform or constant fact of nature. It is an irrefutable theory.
Q.2. Quantitative observation are better in biological method. How?
Answer:
Quantitative observations are considered more accurate than qualitative ones because the former are invariable and measurable and can be recorded in terms of numbers.
THE TERMS TO KNOW